参考博客

前言

如果完全掌握了主席树的前置知识，主席树其实也是一种并不算很难的数据结构（虽然蒟蒻还是花了好久）。主席树主要的前置知识就是权值线段树，一旦理解了权值线段树的相关知识，那么主席树的学习应该也会变得较为简单。

权值线段树

权值线段树是线段树的一种，但是它与普通线段树不同的地方在于，普通线段树节点的区间代表的是序列中的区间，而权值线段树节点的区间则代表了序列中值的区间。
如这样一个序列：1 4 2 3 3
普通线段树中我们通常以序列下标为范围来进行线段树的区间划分，而在权值线段树中这个数组是这样保存的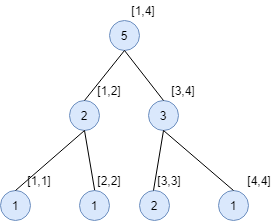：在这里插入图片描述
其中每个节点的值是这个序列在这个值域范围内一共有多少个数。

权值线段树的可加减性

让我们想象这样两颗权值线段树：一颗以序列[1,x]为序列建树，另一颗以[1,n]为基础序列建树，同时都用相同的范围建树，这样的两棵树每个节点所代表的值域是完全相同的。这也就是说，如果我们用第二棵树的某个节点的权值去减去第一棵树对应节点的权值，所得到的值便应该是[x+1,n]序列中该节点值域范围内数的数量，这也就是权值线段树的可加减性。
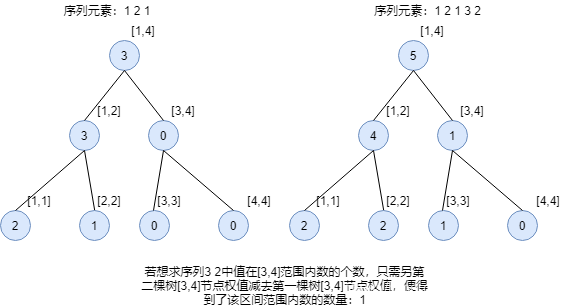
在这里插入图片描述

静态主席树

通过权值线段树及其性质，我们不难想到如何查找区间[l,r]范围的第k大数：只需要针对序列a的每一个前缀都建立一颗权值线段树即可。
然而这样所需要的空间又过于庞大了，需要一定的优化。
通过观察两棵相邻权值线段树的结构，可以发现以下规律：
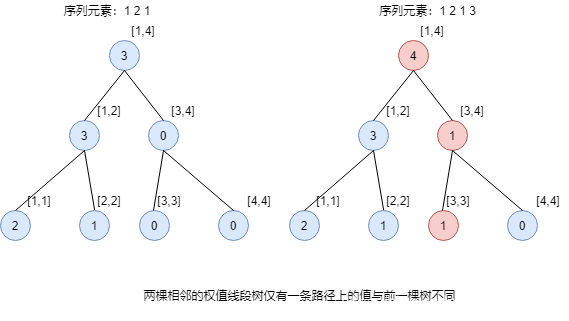
在这里插入图片描述
那么我们就可以让没有变化的节点指向到之前建好的树上，并且新建与前一棵树上不同路径上的节点即可。
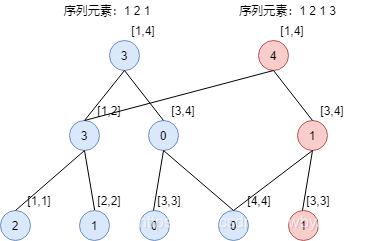
20201024191756154
那么这样我们就得到了建立静态主席树的方法，下面是静态主席树模板题及代码
HDU 2665

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include <bits/stdc++.h>

using namespace std;
typedef long long LL;
#define lson (root << 1)
#define rson (root << 1 | 1)

const int N = 5e6 + 10;
int a[N], b[N];
int T[N], rs[N], ls[N], sum[N], cnt;

void build(int &root, int l, int r) {	
    root = ++cnt;
    sum[root] = 0;
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(ls[root], l, mid);
    build(rs[root], mid + 1, r);
}

void update(int &root, int l, int r, int pre, int data) {
    root = ++cnt;
    ls[root] = ls[pre], rs[root] = rs[pre];
    sum[root] = sum[pre] + 1;
    if (l == r) return;
    int mid = (l + r) >> 1;
    if (data <= mid)
        update(ls[root], l, mid, ls[pre], data);
    else
        update(rs[root], mid + 1, r, rs[pre], data);
}

int query(int s, int e, int l, int r, int k) {
    if (l == r) return l;
    int mid = (l + r) >> 1;
    int Sum = sum[ls[e]] - sum[ls[s]];
    if (k <= Sum)
        return query(ls[s], ls[e], l, mid, k);
    else
        return query(rs[s], rs[e], mid + 1, r, k - Sum);
}

int main() {
    ios::sync_with_stdio(false);
    int t, n, m, q, l, r, k;
    cin >> t;
    while (t--) {
        cin >> n >> q;
        for (int i = 1; i <= n; i++) {
            cin >> a[i];
            b[i] = a[i];
        }
        sort(b + 1, b + n + 1);
        m = unique(b + 1, b + n + 1) - b - 1;
        cnt = 0;
        build(T[0], 1, m);		//建立一棵空树
        for (int i = 1; i <= n; i++)
            a[i] = lower_bound(b + 1, b + m + 1, a[i]) - b;	//离散化后进行下标的对应
        for (int i = 1; i <= n; i++) update(T[i], 1, m, T[i - 1], a[i]);	//每一个数建立一棵树
        while (q--) {
            cin >> l >> r >> k;
            int ans = query(T[l-1],T[r],1,m,k);	//查询
            cout<<b[ans]<<'\n';
        }
    }
    return 0;
}